Inhaltsverzeichnis
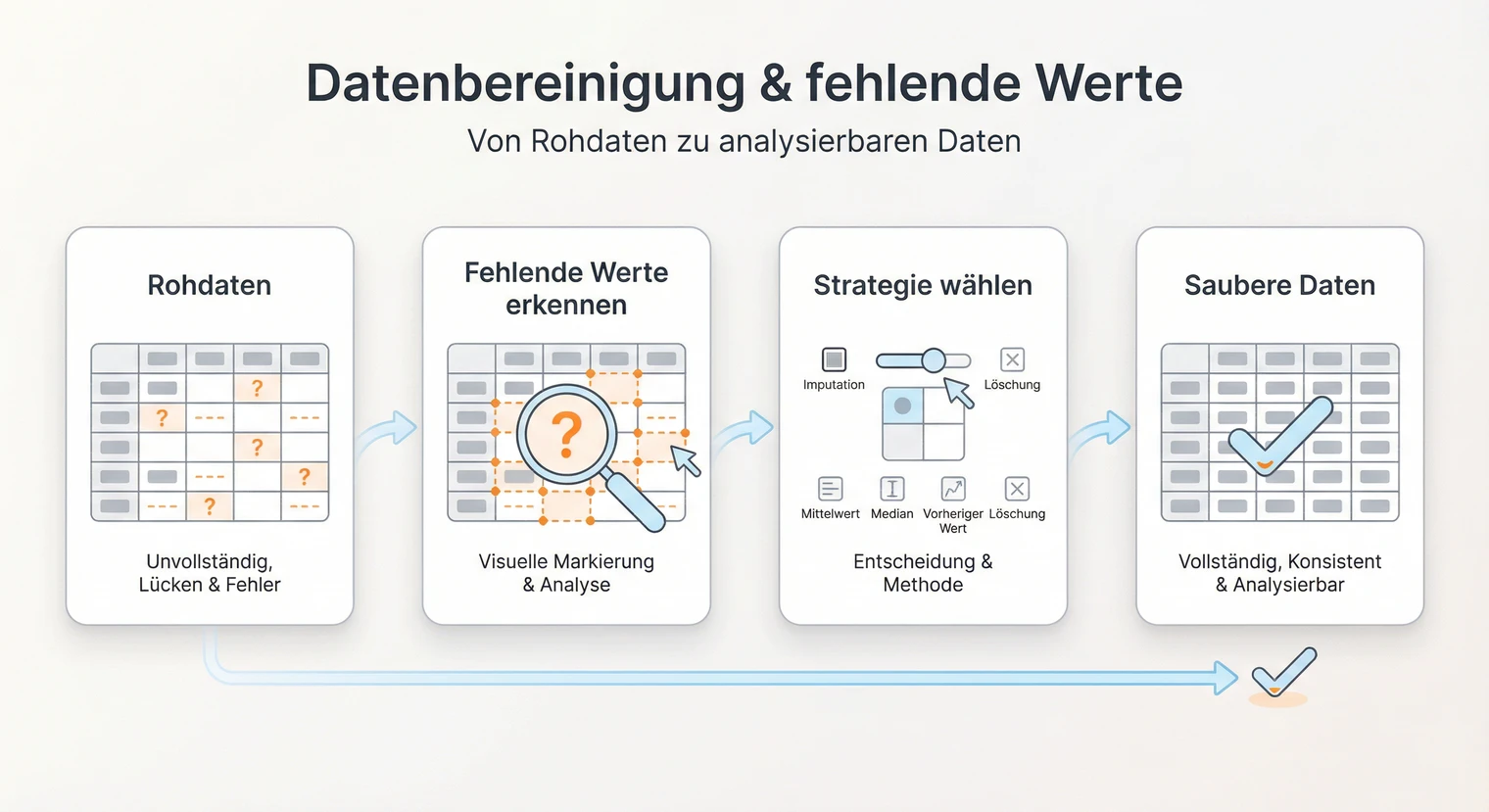
Die Datenbereinigung ist der erste und oft unterschätzte Schritt deiner Datenanalyse. Fehlende Werte, Ausreißer und Eingabefehler können deine Ergebnisse verzerren oder im schlimmsten Fall unbrauchbar machen. Hier erfährst du, wie du fehlende Werte systematisch erkennst, die passende Behandlungsstrategie wählst und alles nachvollziehbar dokumentierst.
Prüfe zuerst den Anteil und das Muster deiner fehlenden Werte. Bei wenigen zufälligen fehlenden Werten (grobe Faustregel: unter 5 %) ist listwise deletion oft vertretbar. Bei mehr fehlenden Werten oder systematischen Mustern kommen Imputation oder Maximum-Likelihood-Verfahren infrage. Dokumentiere jeden Schritt im Methodenteil. Besprich die Strategie im Zweifel mit deiner Betreuung.
Was zählt als fehlender Wert?
Nicht jede Lücke im Datensatz ist ein fehlender Wert im statistischen Sinn. Bevor du mit der Bereinigung startest, musst du unterscheiden, ob Daten tatsächlich fehlen oder ob die Lücke gewollt ist.
Strukturelle Lücken (Design-Missings): Entstehen durch Filterfragen oder logische Abhängigkeiten. Beispiel: „Wie viele Stunden arbeiten Sie pro Woche?" wird nur Erwerbstätigen gestellt. Nicht-Erwerbstätige haben hier keinen fehlenden Wert, sondern die Frage trifft schlicht nicht zu. Diese Fälle werden nicht imputiert, sondern als eigene Kategorie („nicht zutreffend") oder durch Stichprobenteilung behandelt.
Echte fehlende Werte: Die Frage war relevant, wurde aber nicht beantwortet. Beispiel: Eine erwerbstätige Person überspringt die Frage nach den Arbeitsstunden. Hier liegt ein fehlender Wert vor, der behandelt werden muss.
„Weiß nicht" und „Keine Angabe": Diese Antwortoptionen sind ein Sonderfall. Bei Wissens- oder Faktenfragen (z. B. „Wie hoch ist Ihr Nettoeinkommen?") ist „Weiß nicht" oft ein echter fehlender Wert und sollte als solcher behandelt werden. Bei Einstellungsfragen (z. B. „Wie zufrieden sind Sie mit...?") kann „Weiß nicht" dagegen eine inhaltlich relevante Kategorie sein. Prüfe die Fragelogik und entscheide begründet, ob du diese Fälle als fehlende Werte oder als eigene Ausprägung behandelst.
Fehlende-Werte-Codes prüfen: Viele Datensätze nutzen Platzhalter wie 99, -1, -9 oder leere Strings für fehlende Werte. Diese müssen vor der Analyse in das Missing-Format deiner Software umkodiert werden (NA in R, Systemfehlend in SPSS). Sonst werden sie als gültige Werte mitgerechnet und verfälschen deine Ergebnisse.
Workflow: Datenbereinigung in 7 Schritten
Ein systematischer Ablauf hilft dir, nichts zu übersehen und deine Entscheidungen nachvollziehbar zu dokumentieren.
1 Codes identifizieren und umkodieren: Prüfe, ob 99, -1, -9, leere Strings oder andere Platzhalter als fehlende Werte gemeint sind. Kodiere sie in NA (R) bzw. Systemfehlend (SPSS) um.
2 Anteil quantifizieren: Berechne den Anteil fehlender Werte pro Variable und pro Fall. Erstelle eine Übersicht (Tabelle oder Heatmap).
3 Muster visualisieren: Nutze Missing-Pattern-Plots (z. B. naniar::vis_miss() in R oder Missing Value Patterns in SPSS). Erkenne, ob bestimmte Variablen oder Fallgruppen betroffen sind.
4 Muster testen: Führe den Little's MCAR-Test durch und vergleiche Gruppen mit/ohne fehlende Werte in anderen Variablen. Ergänze inhaltliche Argumente für MCAR/MAR.
5 Strategie wählen: Entscheide anhand von Anteil, Muster und Skalenniveau (siehe Entscheidungsmatrix unten).
6 Sensitivitätsanalyse: Führe die Hauptanalyse mit mindestens zwei Strategien durch (z. B. listwise und Imputation) und vergleiche die Ergebnisse.
7 Dokumentieren: Halte im Methodenteil fest: n vor/nach Bereinigung, gewählte Strategie mit Begründung, bei Imputation m und verwendetes Modell, Ergebnis der Sensitivitätsanalyse.
Fehlende Werte klassifizieren: MCAR, MAR, MNAR
Die Wahl der Behandlungsstrategie hängt davon ab, warum Daten fehlen. Die Statistik unterscheidet drei Muster, die unterschiedliche Konsequenzen für deine Analyse haben.
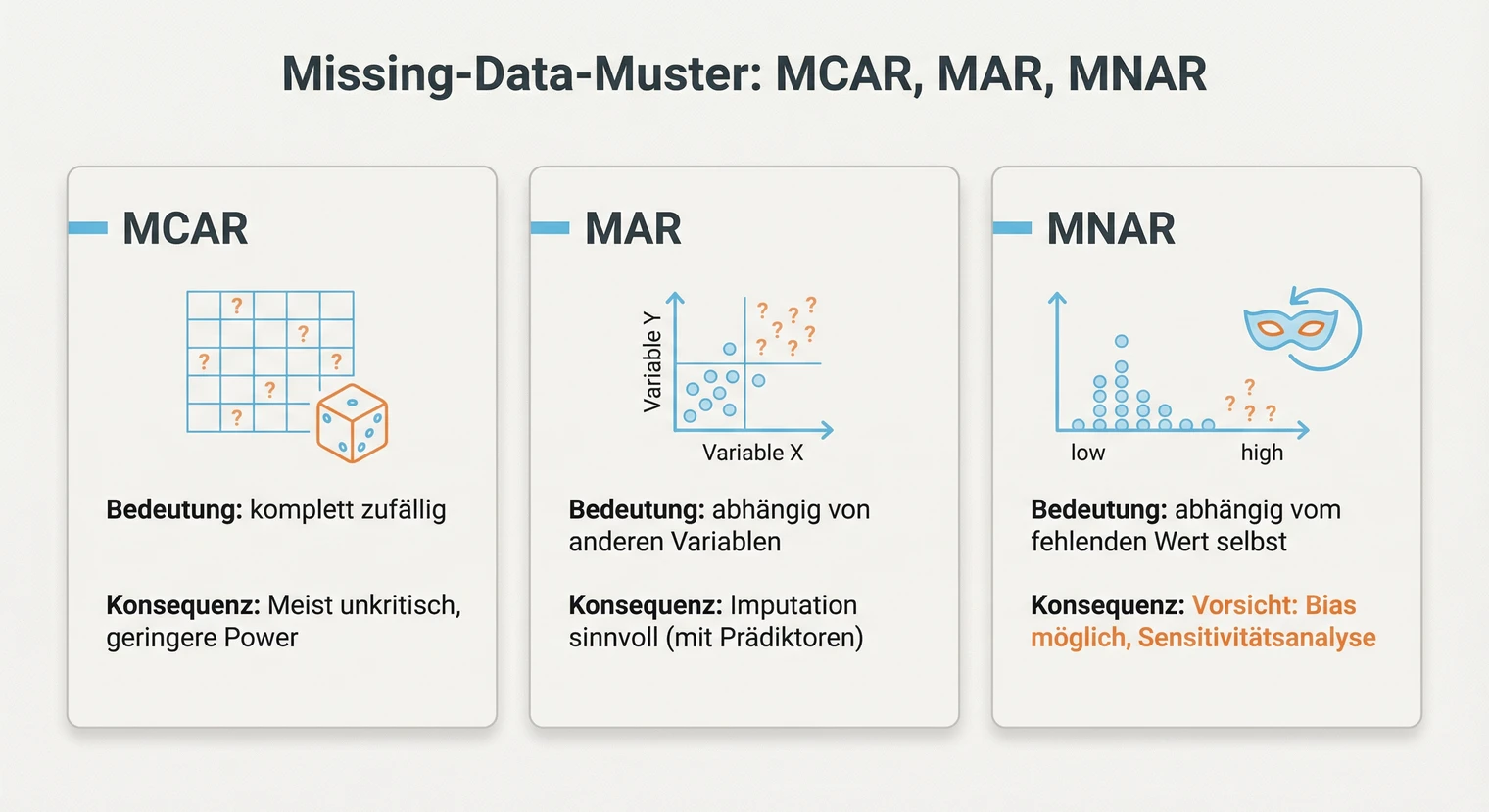
MCAR (Missing Completely At Random): Das Fehlen ist komplett zufällig und hängt weder von der fehlenden Variable selbst noch von anderen Variablen ab. Beispiel: Ein Teilnehmer überspringt versehentlich eine Frage, weil er zu schnell weiterklickt. Bei MCAR sind die verbleibenden Daten repräsentativ. Listwise deletion führt zu Stichprobenverkleinerung, aber nicht zu Verzerrung.
MAR (Missing At Random): Das Fehlen hängt von anderen beobachteten Variablen ab, nicht aber vom fehlenden Wert selbst. Beispiel: Jüngere Befragte beantworten eine Frage zum Einkommen seltener als Ältere. Das Fehlen korreliert mit Alter, nicht mit dem Einkommen selbst. Moderne Verfahren wie multiple Imputation oder FIML liefern unter MAR unverzerrte Schätzer, weil sie die beobachteten Zusammenhänge nutzen.
MNAR (Missing Not At Random): Das Fehlen hängt vom fehlenden Wert selbst ab. Beispiel: Personen mit sehr hohem Einkommen verweigern häufiger die Angabe ihres Einkommens. Standardverfahren (listwise, Imputation, FIML) können bei MNAR zu verzerrten Ergebnissen führen. Du brauchst theoretische Argumente und ggf. Sensitivitätsanalysen. Im Diskussionsteil solltest du MNAR-Risiken als Limitation benennen.
In der Praxis lässt sich MCAR mit dem Little's MCAR-Test prüfen. Ein nicht signifikanter Test beweist MCAR allerdings nicht – er macht es nur plausibel (bei kleinen Stichproben hat der Test wenig Power). Kombiniere den Test daher mit Musterplots und Gruppenvergleichen. Die Unterscheidung zwischen MAR und MNAR ist rein statistisch nicht möglich. Hier brauchst du inhaltliche Überlegungen: Warum könnten die Daten fehlen? Sensitivitätsanalysen sind hier der Standard. Dokumentiere deine Einschätzung und begründe, warum du MAR für plausibel hältst.
Strategien für den Umgang mit fehlenden Werten
Die richtige Strategie hängt von Anteil, Muster und Skalenniveau ab. Die folgende Matrix hilft dir bei der Entscheidung.
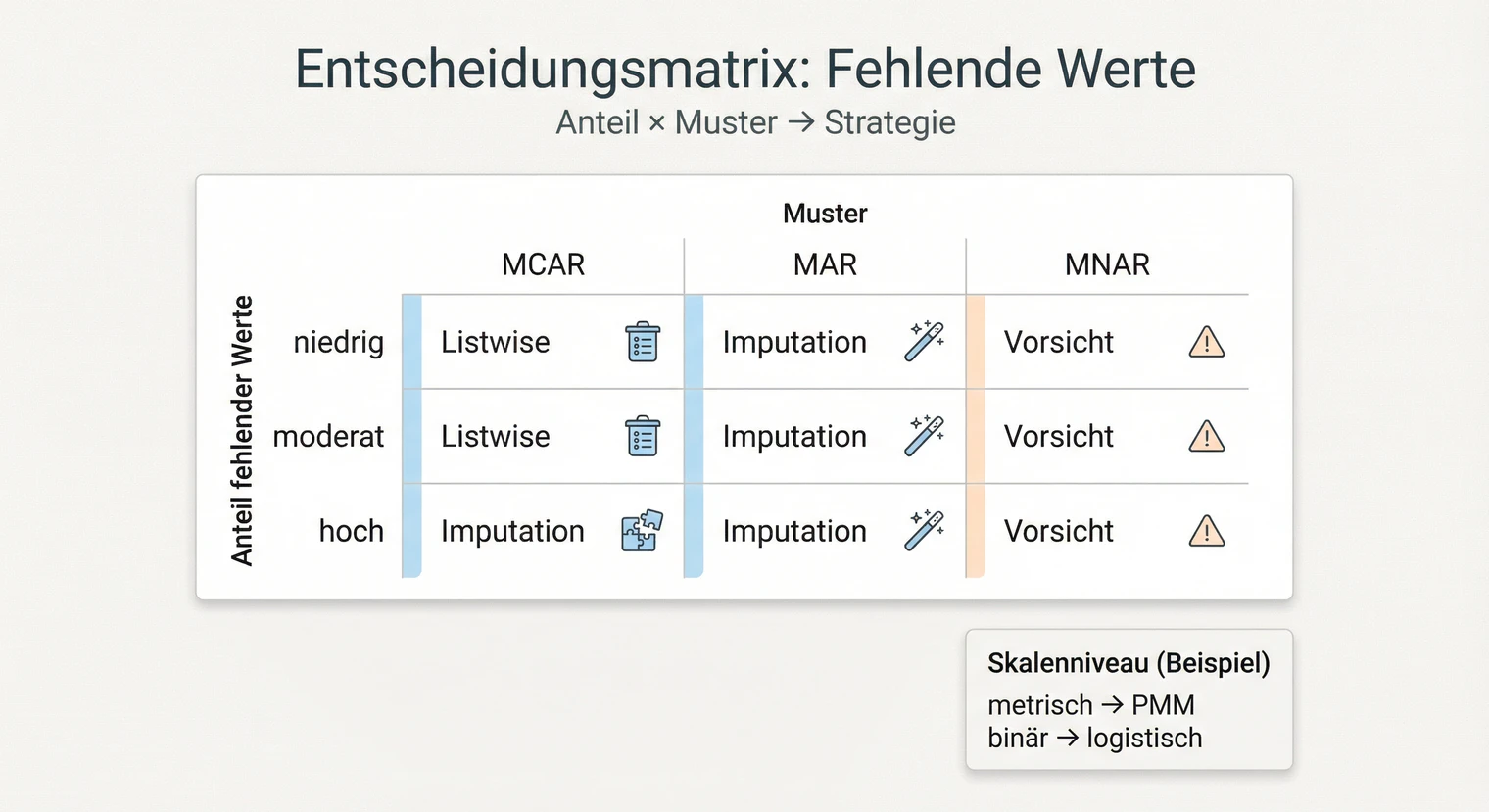
Anteil niedrig (ca. < 5 %) + MCAR plausibel
Listwise deletion oft vertretbar, wenn wenige Variablen betroffen sind und der Fallverlust gering bleibt. Keine Verzerrung bei MCAR. Prüfe das resultierende n nach Complete-Case-Analyse.
Anteil moderat (ca. 5–30 %) + MAR plausibel
Multiple Imputation oder FIML. Nutzt alle verfügbaren Informationen, bei MAR unverzerrte Schätzer. Bei metrischen Variablen PMM, bei binären logistische Imputation.
Anteil hoch (ca. > 30 %) oder MNAR wahrscheinlich
Vorsicht: Auch Imputation kann verzerrt sein. Prüfe zuerst: Sensitivitätsanalyse mit verschiedenen Strategien, alternative Modellspezifikation, Fragelogik und Skalierung überdenken. Variablenausschluss ist der letzte Ausweg, nicht die erste Lösung. Bedenke: Ein Ausschluss verändert die Forschungsfrage und muss inhaltlich begründet werden. MNAR-Risiko immer als Limitation benennen.
Skalenniveau beachten
Metrisch: PMM (Predictive Mean Matching) oder Regression. Binär: Logistische Imputation. Ordinal: Proportional Odds oder ordinale logistische Modelle.
Wichtig: Die Prozentangaben sind Richtwerte, keine festen Grenzen. Welche Strategie angemessen ist, hängt auch vom Fach, Modell und der Betreuung ab. Besprich deine Entscheidung im Zweifel vorab. Nicht empfohlen: Mittelwert-Ersetzung, pairwise deletion, single Imputation ohne Unsicherheitsberücksichtigung.
Sensitivitätsanalysen sind unabhängig von der gewählten Strategie wichtig. Führe die Hauptanalyse mit mindestens zwei Ansätzen durch (z. B. listwise und Imputation). Wenn die Ergebnisse konvergieren, stärkt das deine Schlussfolgerungen. Wenn nicht, berichte beide Varianten und diskutiere die Unterschiede.
Multiple Imputation: Modelle und Diagnostik
Multiple Imputation (MI) ersetzt jeden fehlenden Wert mehrfach auf Basis der vorhandenen Daten. Die Analysen werden auf allen imputierten Datensätzen durchgeführt und die Ergebnisse nach Rubin's Rules kombiniert. Der Vorteil: Die Unsicherheit der Schätzung wird berücksichtigt.
PMM (Predictive Mean Matching): Standard für metrische Variablen. Imputiert nur beobachtete Werte, respektiert daher die empirische Verteilung. Robust bei leichten Verletzungen der Normalverteilungsannahme.
Logistische Imputation: Für binäre Variablen (0/1, ja/nein). Schätzt die Wahrscheinlichkeit und zieht daraus den imputierten Wert.
Proportional Odds / ordinale logistische Modelle: Für ordinale Variablen (Likert-Skalen als Einzelitems). Berücksichtigt die Rangfolge der Kategorien.
Tipp: In R wählt das mice-Paket automatisch passende Modelle basierend auf dem Variablentyp. Prüfe die Auswahl und passe sie bei Bedarf an.
FIML oder Multiple Imputation? FIML (Full Information Maximum Likelihood) ist eine Alternative zu MI und besonders geeignet, wenn dein Hauptmodell ohnehin mit Maximum Likelihood geschätzt wird (z. B. Strukturgleichungsmodelle in lavaan oder Mplus). FIML schätzt Parameter und Missing-Handling in einem Schritt und erfordert keine separaten imputierten Datensätze. MI ist flexibler, wenn du verschiedene Analyseverfahren nutzt oder die Daten vor der Analyse explorativ erkunden willst. Beide Verfahren liefern unter MAR unverzerrte Schätzer. Einschränkung: Je nach Software kann FIML bei fehlenden Werten in exogenen Variablen (unabhängige Variablen ohne Residuum im Modell) Probleme bereiten. Prüfe die Dokumentation deines Tools; im Zweifel MI oder eine Modellanpassung (z. B. exogene als endogene Variable modellieren).
Wie viele Imputationen (m)? Früher galten m = 5 als ausreichend. Neuere Empfehlungen orientieren sich am Anteil fehlender Werte: Als Faustregel sollte m mindestens dem prozentualen Anteil entsprechen (z. B. m = 20 bei 20 % fehlenden Werten). Bei komplexen Analysen sind m = 20–50 üblich. Das sind Richtwerte, keine festen Regeln. Mehr Imputationen erhöhen die Stabilität der Schätzer, aber auch die Rechenzeit. Im Zweifel mit der Betreuung abstimmen.
Verteilungen vergleichen: Plotte beobachtete vs. imputierte Werte. Die Verteilungen sollten ähnlich sein. Starke Abweichungen deuten auf Modellprobleme hin.
Konvergenz prüfen: Bei MICE sollte die Konvergenz der Kettenplots (trace plots) geprüft werden. Keine klaren Trends = gut.
Plausibilität: Liegen die imputierten Werte im sinnvollen Bereich? Ein imputiertes Alter von 150 Jahren deutet auf ein Problem hin.
Imputationsmodell vollständig aufbauen: Nimm alle Variablen ins Imputationsmodell auf, die (a) in deiner Analyse vorkommen und (b) die Missingness erklären könnten. Fehlen relevante Prädiktoren, droht Bias unter MAR.
Design-Missings nicht imputieren: Stelle sicher, dass strukturelle Lücken (Filterfragen, „nicht zutreffend") nicht imputiert werden. In mice steuerst du das über eine where-Matrix:
# where-Matrix: TRUE = imputieren, FALSE = nicht imputieren
where_matrix <- is.na(daten)
# Design-Missings ausschließen (z. B. Arbeitsstunden für Nicht-Erwerbstätige)
where_matrix[daten$erwerbstaetig == 0, "arbeitsstunden"] <- FALSE
imp <- mice(daten, m = 20, where = where_matrix)
Ohne diese Maske erzeugt mice künstliche Werte, wo gar keine fehlen – das verfälscht deine Daten.
Ausreißer identifizieren und behandeln
Neben fehlenden Werten gehören Ausreißer zur Datenbereinigung. Ein Ausreißer ist ein Wert, der ungewöhnlich weit vom Rest der Verteilung entfernt liegt. Das kann ein Eingabefehler sein, aber auch ein echter Extremfall.
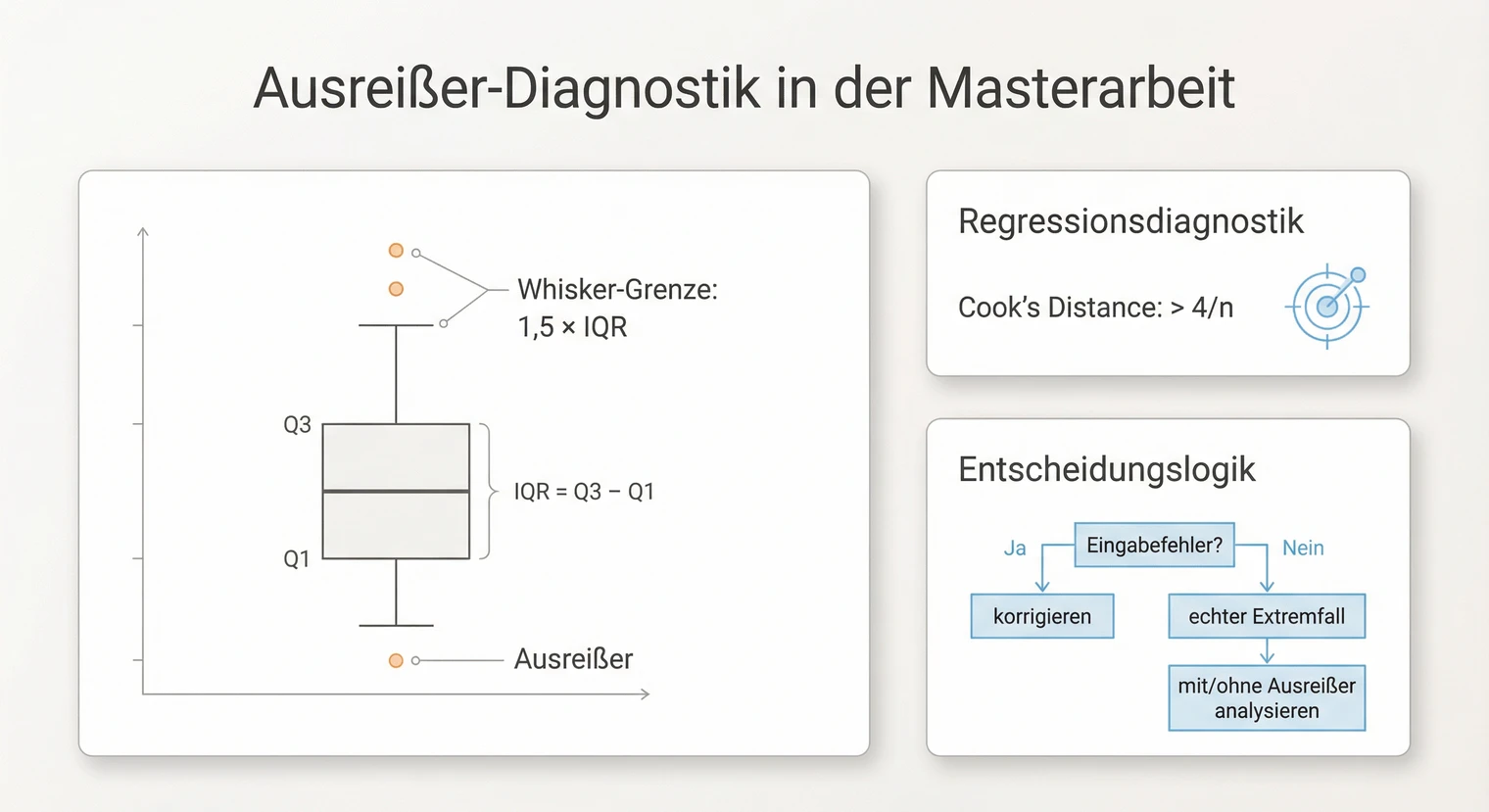
Identifikation: Boxplots zeigen Werte außerhalb der Whisker (1,5-facher Interquartilsabstand) als potenzielle Ausreißer. Bei Regressionen liefern Cook's Distance und standardisierte Residuen zusätzliche Hinweise. Gängige Richtwerte sind Cook's D > 4/n und Residuen > |3|. Nutze diese Schwellen als Startpunkt, danach immer inhaltlich prüfen und dokumentieren. Ob ein Wert problematisch ist, hängt vom Kontext ab: Ein Alter von 150 Jahren ist offensichtlich ein Fehler, ein Alter von 85 Jahren kann dagegen ein valider Extremfall sein.
Behandlung: Automatisches Löschen von Ausreißern ist keine gute Strategie. Prüfe zunächst, ob ein Eingabefehler vorliegt. Wenn ja, korrigiere den Wert oder setze ihn auf fehlend. Bei echten Extremfällen führst du die Analyse mit und ohne den Ausreißer durch. Wenn die Ergebnisse stabil bleiben, behältst du den Wert. Wenn nicht, dokumentiere beide Varianten und begründe deine finale Entscheidung.
Software-Tools: SPSS und R konkret
Hier findest du konkrete Anleitungen für die gängigsten Tools. Kopiere die Menüpfade bzw. den Code und passe ihn an deine Daten an.
Fehlende Werte definieren: Variablenansicht → Spalte „Fehlend" → Werte wie 99, -1 als fehlend markieren.
Missing-Analyse: Analysieren → Fehlende Werte → Variablen auswählen → „EM" und „Little's MCAR-Test" aktivieren → OK.
Multiple Imputation: Analysieren → Multiple Imputation → Fehlende Werte imputieren → Methode „Automatisch" oder „PMM" → Anzahl Imputationen (m) festlegen → Ausgabe-Datensatz benennen.
Ausreißer: Analysieren → Deskriptive Statistiken → Explorative Datenanalyse → Diagramme → Boxplots aktivieren.
Für den Methodenteil: Exportiere die EM-Ausgabe und den MCAR-Test (χ², df, p). Bei Imputation: Nenne m und die Methode.
Missing-Pattern visualisieren:
library(naniar)
vis_miss(daten) # Heatmap fehlender Werte
gg_miss_var(daten) # Anteil pro Variable
Little's MCAR-Test:
# Option 1: naniar
library(naniar)
mcar_test(daten) # gibt chi², df, p aus
# Option 2: BaylorEdPsych (falls naniar nicht funktioniert)
library(BaylorEdPsych)
LittleMCAR(daten) # Dataframe übergeben, gibt chi², df, p aus
Wichtig zur Interpretation: Ein nicht signifikanter Test beweist MCAR nicht – er macht es nur plausibel. Bei kleinen Stichproben hat der Test wenig Power. Ergänze daher immer Gruppenvergleiche und Musterplots. Falls dein Paket die Funktion nicht kennt, wähle eine der beiden Alternativen oben.
Multiple Imputation mit mice:
library(mice)
imp <- mice(daten, m = 20) # mice wählt Methoden nach Variablentyp
imp$method # prüfe die gewählten Methoden
fit <- with(imp, lm(y ~ x1 + x2))
pool(fit) # Ergebnisse kombinieren
Wichtig: mice wählt automatisch passende
Methoden (pmm für metrisch, logreg für binär, polr für ordinal). Prüfe mit imp$method, ob die Auswahl für deine Daten sinnvoll ist. Bei Bedarf kannst du einzelne Methoden anpassen.
Dokumentation und Reporting
Eine saubere Dokumentation macht deine Datenbereinigung nachvollziehbar. Im Methodenteil beschreibst du das Vorgehen, im Ergebnisteil berichtest du Sensitivitätsanalysen, in der Diskussion benennst du Limitationen.
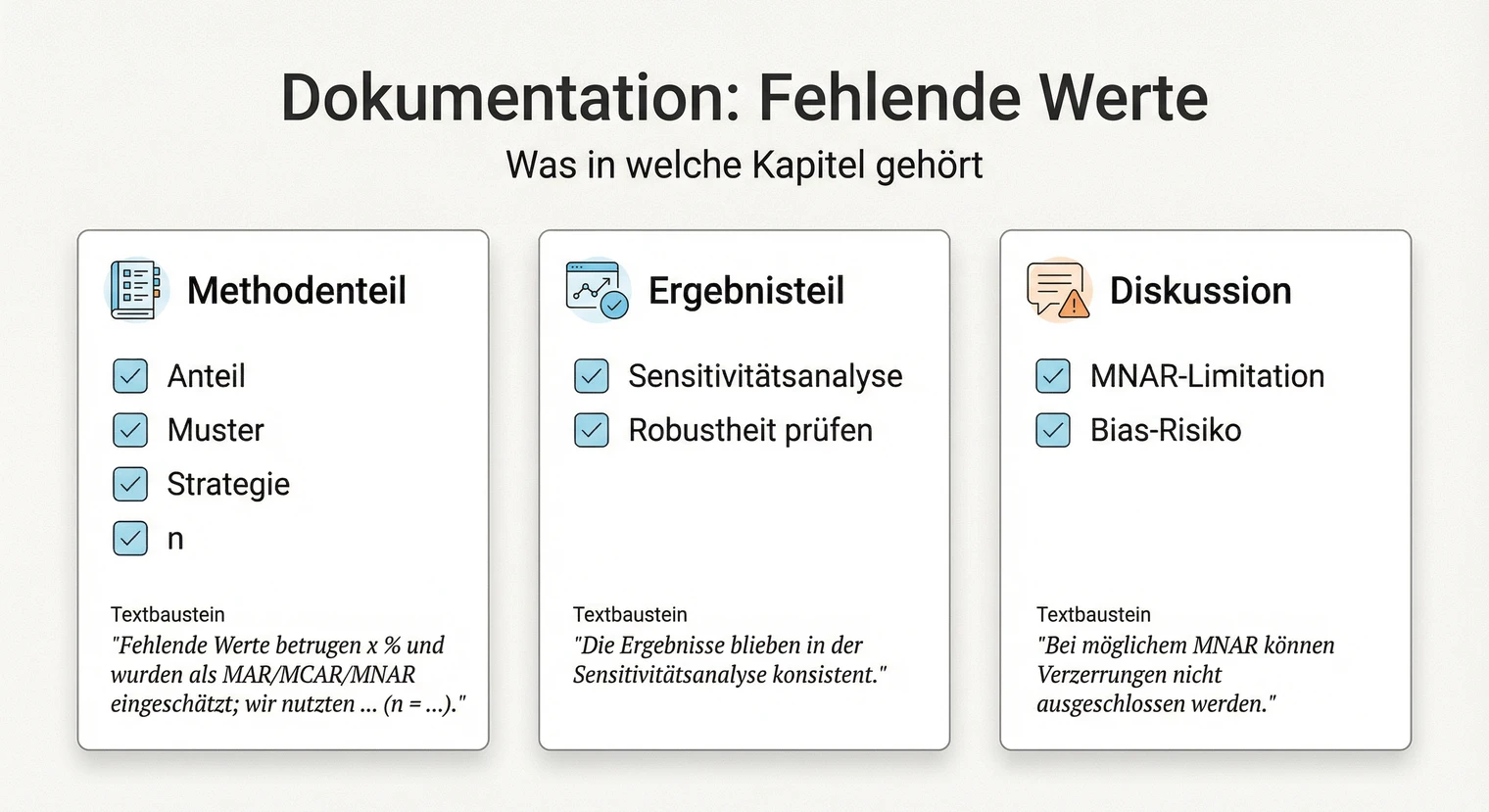
Methodenteil (listwise deletion)
„Vor der Analyse wurden die Rohdaten auf Vollständigkeit geprüft. Der Anteil fehlender Werte lag zwischen [Min] % und [Max] % (M = [Mittelwert] %). Der Little's MCAR-Test war nicht signifikant, χ²([df]) = [Wert], p = [p-Wert]. In Kombination mit den Musterplots und Gruppenvergleichen wurde MCAR als plausibel eingeschätzt. Aufgrund des geringen Anteils wurden Fälle mit fehlenden Werten bei zentralen Variablen ausgeschlossen (listwise deletion). Die finale Stichprobe umfasst n = [Stichprobengröße]."
Methodenteil (mit Imputation)
„Fehlende Werte (M = [Anteil] %) wurden mittels multipler Imputation behandelt (mice-Paket in R, m = [Anzahl], PMM für metrische, logistische Imputation für binäre Variablen). Der Little's MCAR-Test war signifikant, χ²([df]) = [Wert], p = [p-Wert]. Gruppenvergleiche zeigten, dass [Gruppe] häufiger Angaben zu [Variable] verweigerte. MAR wurde daher als plausibel angenommen."
Ergebnisteil (Sensitivitätsanalyse)
„Zur Prüfung der Robustheit wurde die Hauptanalyse zusätzlich mit listwise deletion durchgeführt. Die Ergebnisse waren konsistent: Der Effekt von [UV] auf [AV] blieb signifikant (MI: β = [Wert], p = [p]; listwise: β = [Wert], p = [p]). Die Schlussfolgerungen bleiben von der Wahl der Missing-Strategie unberührt." (Alternativ bei divergenten Ergebnissen: beide berichten und diskutieren.)
Diskussion (MNAR-Limitation)
„Eine Einschränkung betrifft die fehlenden [Variable]-Angaben. Obwohl MAR auf Basis der beobachteten Zusammenhänge plausibel erscheint, kann MNAR nicht ausgeschlossen werden: [Beschreibung des möglichen systematischen Ausfalls]. In diesem Fall wären auch die imputierten Werte verzerrt. Die Sensitivitätsanalyse zeigte jedoch [robuste/abweichende] Ergebnisse."
Missing-Codes nicht umkodieren: Werte wie 99 oder -1 werden als gültige Daten mitberechnet. → Vor jeder Analyse alle Codes in NA/Systemfehlend umwandeln.
Muster nicht prüfen: Listwise deletion bei MAR/MNAR verzerrt die Stichprobe. → Immer Little's MCAR-Test durchführen und Gruppenvergleiche machen.
Design-Missings imputieren: Filterfragen-Lücken sind keine echten fehlenden Werte. → Strukturelle Lücken separat behandeln, nicht imputieren.
Keine Sensitivitätsanalyse: Eine einzige Strategie lässt Unsicherheit offen. → Mindestens zwei Ansätze vergleichen und berichten.
Nächste Schritte
Wenn deine Daten bereinigt sind, folgt die eigentliche Analyse. Mit sauberen Daten kannst du dich auf die inhaltlichen Fragen konzentrieren, statt dich mit technischen Problemen herumzuschlagen.
Der nächste Schritt ist die Datenanalyse. Dort wählst du das passende Verfahren für deine Forschungsfrage, prüfst die Voraussetzungen und führst die inferenzstatistischen Tests durch.
Falls du mit Statistik noch unsicher bist, hilft dir der entsprechende Ratgeber bei der Auswahl des richtigen Verfahrens. Für die Darstellung der Ergebnisse findest du dort Formulierungsbausteine und Reporting-Checklisten.
Wenn deine Arbeit inhaltlich fertig ist und du sie drucken und binden lassen möchtest, kannst du das bei BachelorHero online konfigurieren.
Häufig gestellte Fragen
Ab welchem Anteil fehlender Werte wird es problematisch?
Eine feste Grenze gibt es nicht. Die oft genannten Richtwerte (< 5 % unkritisch, > 30 % problematisch) sind Orientierung, keine starren Regeln. Entscheidender als der reine Prozentsatz ist das Muster: Systematische fehlende Werte (MNAR) können schon bei wenigen Prozent problematisch sein, während zufällige Ausfälle (MCAR) auch bei höherem Anteil handhabbar sind. Im Zweifel: Betreuung fragen.
Wie erkenne ich, ob meine fehlenden Werte zufällig sind?
Nutze den Little's MCAR-Test (SPSS: Analysieren → Fehlende Werte; R: naniar::mcar_test()). Ist er nicht signifikant, macht das MCAR plausibel – beweisen kann er es nicht (Power-Problem bei kleinen Stichproben). Ergänze Gruppenvergleiche und Musterplots. Wichtig: MAR vs. MNAR ist statistisch nicht trennbar. Für MAR brauchst du inhaltliche Argumente, warum das Fehlen nicht vom fehlenden Wert selbst abhängt. Sensitivitätsanalysen sind hier der Standard.
Was mache ich mit Codes wie 99 oder -1 im Datensatz?
Viele Datensätze nutzen Platzhalter wie 99, -1, -9 oder leere Strings für fehlende Werte. Bevor du analysierst, musst du diese in das Missing-Format deiner Software umkodieren: NA in R, Systemfehlend in SPSS. Sonst werden sie als gültige Werte mitgerechnet. Prüfe im Codebuch oder der Dokumentation, welche Codes verwendet wurden.
Wann ist „Weiß nicht" ein fehlender Wert, wann eine eigene Kategorie?
Das hängt von der Fragelogik ab. Bei Faktenfragen (z. B. Einkommen, Alter) ist „Weiß nicht" meist ein echter fehlender Wert. Bei Einstellungsfragen (z. B. Zufriedenheit) kann es eine inhaltlich relevante Antwort sein, etwa wenn echte Ambivalenz vorliegt. Entscheide begründet und dokumentiere deine Entscheidung im Methodenteil.
Wie gehe ich mit Filterfragen und Design-Missings um?
Strukturelle Lücken durch Filterfragen (z. B. Arbeitsstunden nur für Erwerbstätige) sind keine echten fehlenden Werte. Imputiere sie nicht. Behandle sie als eigene Kategorie („nicht zutreffend") oder teile die Stichprobe. Bei Imputation: Stelle sicher, dass Design-Missings nicht imputiert werden (z. B. über eine where-Maske in mice).
Wie wähle ich die Anzahl der Imputationen (m)?
Früher galten m = 5 als ausreichend. Neuere Empfehlungen orientieren sich am Anteil fehlender Werte: m sollte mindestens dem prozentualen Anteil entsprechen (z. B. m = 20 bei 20 % fehlenden Werten). Bei komplexen Analysen sind m = 20–50 üblich. Mehr Imputationen erhöhen die Stabilität, aber auch die Rechenzeit. Besprich die Wahl mit deiner Betreuung.
Wie prüfe ich, ob die Imputation gut funktioniert hat?
Drei Checks: (1) Verteilungen vergleichen: Plotte beobachtete vs. imputierte Werte, sie sollten ähnlich sein. (2) Konvergenz prüfen: Bei MICE die Kettenplots (trace plots) anschauen, keine klaren Trends = gut. (3) Plausibilität: Liegen imputierte Werte im sinnvollen Bereich? Ein Alter von 150 Jahren deutet auf ein Problem hin.
Was ist der Unterschied zwischen listwise und pairwise deletion?
Listwise deletion entfernt alle Fälle mit mindestens einem fehlenden Wert. Die Stichprobe wird kleiner, aber alle Analysen basieren auf denselben Fällen. Pairwise deletion nutzt alle verfügbaren Daten pro Variablenpaar, führt aber zu unterschiedlichen Stichprobengrößen je Analyse. Pairwise deletion kann zu inkonsistenten Ergebnissen führen und wird meist nicht empfohlen.
Weitere interessante Artikel 
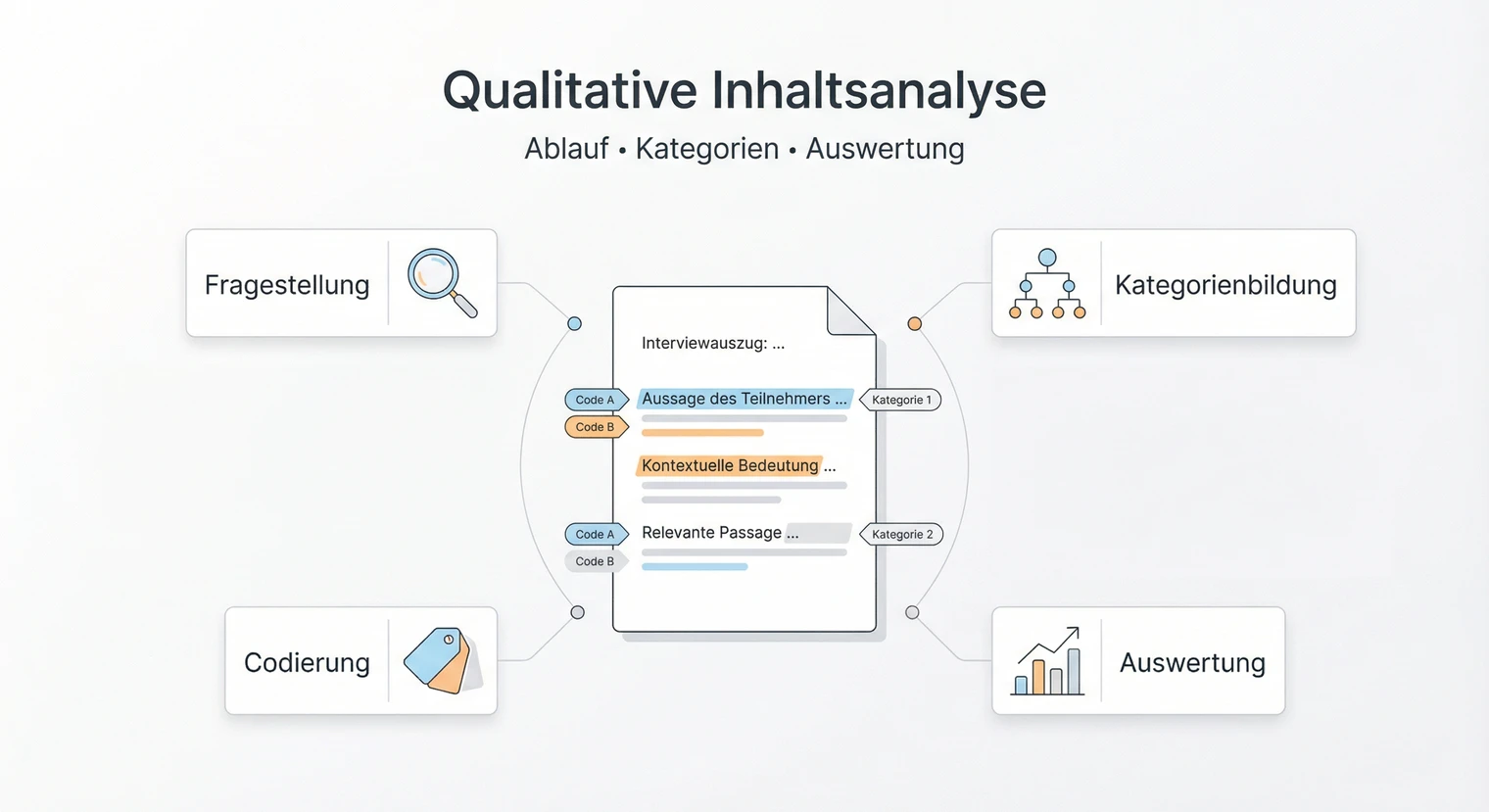Qualitative Inhaltsanalyse 
Seitenzahlen richtig einfügen 
Wissenschaftlicher Schreibstil